This research pursues the development of a computational model for underwater blast (UNDEX) on surrogate lung models. Initial experiments, which were conducted by NSMRL and reported by Guzas et al. (2019), are intended to measure the response of surrogate lung models to UNDEX for the purpose of establishing reliable safe standoff distances for Explosive Ordnance Disposal (EOD) personnel and others at risk of exposure to UNDEX. The computational models, which are to be integrated into the Pulmo software, are to be used to aid in interpreting the surrogate lung model response and as a tool to estimate human injury risk due to UNDEX.
Underwater Blast Experiments (UNDEX)
The computational model is intended to model the initial UNDEX-ball experiments, which were conducted by initiating small detonator charges near a lung-sized air-filled rubber ball (D=~25.0 cm) while submerged inside a water tank. To quantify and compare with the experiments, ball compaction and expansion displacements and interior ball pressures are of interest for the numerical analyses. The magnitude of UNDEX-induced volume changes of the lungs (and surrogates) is believed to be correlate to injury risk.

Details of the UNDEX experiments are described by Guzas et al 2019. The experiments were instrumented with an array of pressure sensors to measure the pressure-time loading near the ball in addition to the internal pressure of the ball after excited by the UNDEX loads. High-speed videos were used to image the ball during the UNDEX event, and through the use of Digital Image Correlation (DIC) analysis, displacement and strain-fields on the surface of the ball were also obtained. The ball was pressurized close to 1.0 psi prior to submersion in the tank. The replicate experiments Test 1-5 reported by Guzas et al. 2019 are of interest, which used a RP-80 detonator placed at a distance of 48.3 cm from the ball to generate the UNDEX loads in the configurations.

Dynamic material characterization test for calibrating constitutive models for the ball material
Underwater Blast Experiments (UNDEX)
UNDEX events generate complex dynamic loads, so, to physically model the ball responses, dynamic material characterization tests are needed for calibrating constitutive models for the ball material.
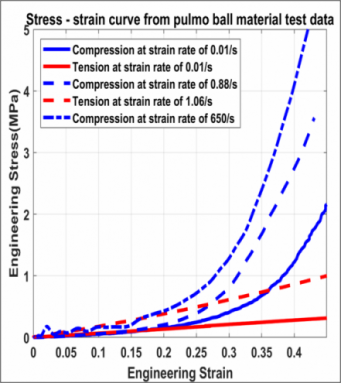
With samples obtained from the same manufacturer and product name for the ball, dynamic material characterization experiments were conducted at various strain-rates using K&C’s quasi-static servo-electric loader and K&C’s ¾” split-Hopkinson Pressure Bar (SHPB) machine in both tension and compression. The servo-electric loader was used to load the ball material in tension and compression and measure the stress-strain responses of the ball material at target strain rates of 0.01/s and 1.0/s. The SHPB apparatus was used to load the ball material under dynamic compression at the higher target strain rates of 1,000/-10,000/s.
The figure right shows some of the ball material property data, which points to several of the most important material behaviors that were presented by the ball material in our laboratory experiments:
- The response of the material is highly sensitive to the rate of loading. As shown, the material is much stiffer under faster rates of loading. For context, the strain-rates generated in the UNDEX-ball experiment is anticipated to be in the range of 1-100/s, based on evidence from the DIC;
- The material exhibits both viscoelastic and nonlinear elastics behaviors, depending on the strain-level. At small strains, e.g., less than 10%, viscoelastic behaviors are evident. At larger strains, the material appears to exhibit nonlinear elastic behaviors;
- The nonlinear behaviors are much more pronounced in compression than in tension. Locking of the stress-strain response in compression at over 20% strain, but not in tension.
Computational Model
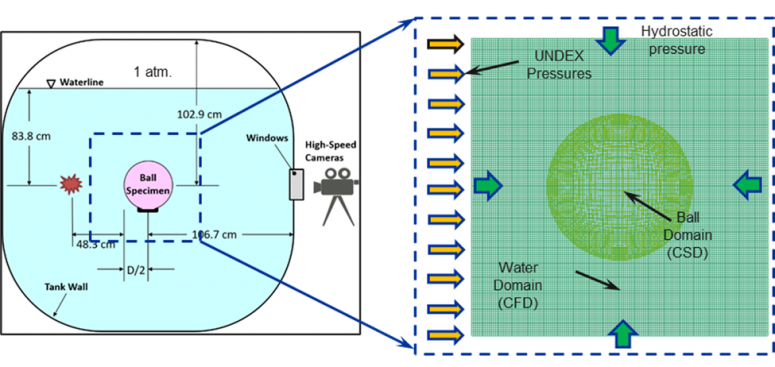
As the ultimate objective of this research is to produce efficient high-fidelity methods and models for UNDEX events, a small compact portion of the fluid domain is modeled with the ball submerged in it. As illustrated below, the computational model consists of a Lagrangian Computational Solid Dynamic (CSD) model for the lung-sized rubber ball, which is coupled to an Eulerian Computational Fluid Dynamics (CFD) model/domain for the water and air using a Fluid-Structure Interaction (FSI) scheme. For the Eulerian CFD domain, the multi -material Arbitrary Lagrangian-Eulerian (ALE) method and solver in LS-DYNA is used to treat both the water and air (the latter inside of the ball). The CFD domain is modeled as a 50.8 cm cube centered at the ball center.
Coupled Lagrangian Computational Solid Dynamic (CSD) and Eulerian Computational Fluid Dynamics (CFD) Model
The Lagrangian CSD domain uses a finite element discretization of the ball itself. The ball is discretized with fully integrated hexahedral finite elements having one element through-the-thickness of the ball since the ball is very thin and includes representations of the cap and cabling system used to restrain the ball in the tank. The ball properties are taken directly from measurements on balls obtained and tested in the laboratory. The ball thickness and density are taken as t = 1.2 mm (0.047 in nominal) and 0.733 g/cc.
Both domains are shown above and are coupled using a penalty- based FSI algorithm between the water/air interfaces and the CSD ball domain to solve the coupled FSI computational problem.
Assumptions
- Ball initial deformation idealized/initialized to the hydrostatic pressure 15.89 psi (ambient + depth)
- Air behaves as an ideal gas
- UNDEX event generates spherical shock waves and the experimental records are used as truth
- The fluid in the tank behaves like in an open area infinite domain
Boundary conditions and initial conditions
- On CFD domain, all surfaces applied hydrostatic pressure of 15.89 psi (ambient + depth)
- On CFD domain, non-reflective boundary conditions on all but the loaded surfaces
- On CSD domain, the ends of all the restraint cables fixed
Material laws
- Linear polynomial equation-of-state for air and water
- Various material models for the ball, including a Prony series viscoelastic law fit to the lab data
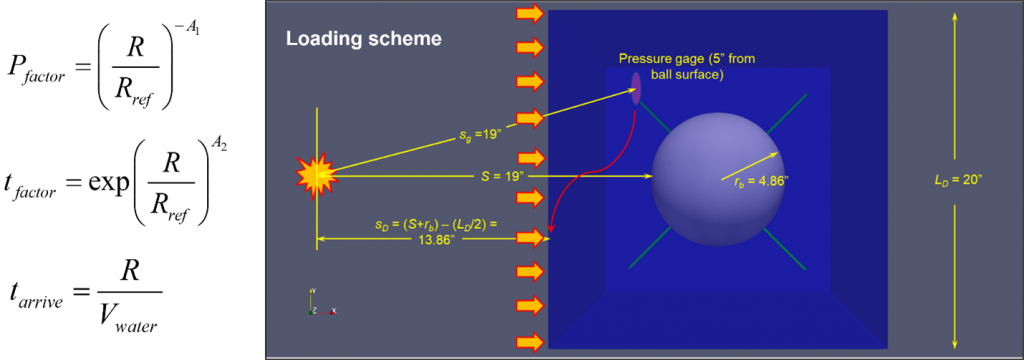
UNDEX loading scheme: SSL (Scaled Spherical Loading) scheme
The experimentally-measured UNDEX pressure record is scaled to be applied as pressure-time histories over loading segments on one face of the CFD domain (see below figure)This prototype method applies Cole’s scaling at each of the individual load curves created for each point/segment on the water surface, modifying the amplitude, duration, and time-of-arrival (TOA) of the pulse. We intend in this method to mimic the actual spherical UNDEX loading on the front face of the domain by applying the experimentally obtained UNDEX pressure histories to the computational model. The pressure amplitude, duration and TOA are scaled as follows:
Computational Results
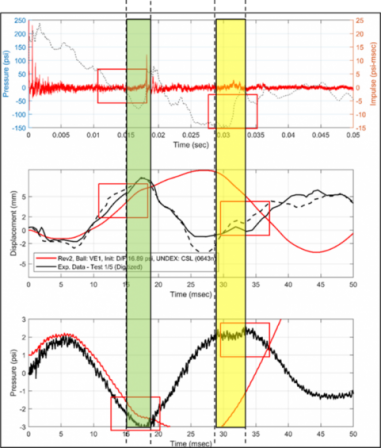
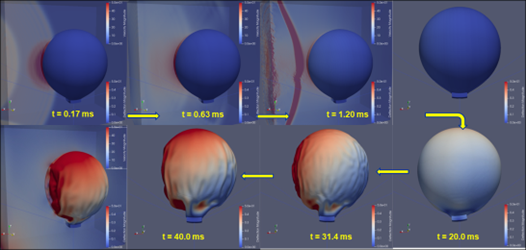
Like the experiments, the computational model predicts an initial compaction of the ball, which peaks at about 7.5 ms, followed by a rapid expansion of the ball to a peak about 10 ms later (17-20 ms). The ball then recontracts, causing at least two large cycles of volume change in the air-ball system. Snapshots from the computational model are shown above, which are colored by both ball deformation and the pressures in the water surrounding the ball.
The figure right plots the applied UNDEX pressures/impulses (top), the displacement at the center of the ball (center), and the ball internal gage pressure (bottom) from both the experiment (black) and the computational model (red). Good correlations are observed between the two for the initial compaction and first ball expansion (at 17-20 ms). However, the computational model begins to deviate from the experimental records near the peak of the second ball contraction, which occurs at the same time UNDEX pressure records show a second major increase in impulse (potentially from the first UNDEX bubble loading).
Conclusions
Three key outcomes can be reported at this time from this work:
- A coupled CSD/CFD model developed for the UNDEX-ball experiment predicts the volume changes observed in experiments.
- The current model and methods provides good predictions of the displacement and internal pressure in the air-filled ball system during the initial compaction and first expansion of its response.
- The UNDEX loading is highly coupled with the ball/lung system response
FUTURE WORK
- Evaluate and improve the models and parameters identified to affect the computed ball-air system response, especially after the second impulse delivery.
- Improve the UNDEX loading characterization methods.
- Extend the models for future experiments using more anatomically-detailed lung and torso surrogate models.
REFERENCE
Guzas, S. Turner, M. Babina, B. Casper, T. Fetherston and J. Ambrico, “Validation of a Surrogate Model for Marine Mammal Lung Dynamics under Underwater Explosive Impulse,” in Proc. ASME 2019 V&V Symp., Las Vegas, NV, 2019.
DISCLAIMER
This material is based upon work supported by the US Army Medical Research and Development Command (USAMRDC) or U.S. Army Medical Research Acquisition Activity (USAMRAA) under Contract No.W81XWH22C0078. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the USAMRDC or USAMRAA.
